You can find python implementation of all activation functions
here
What is an activation function ?
- Decide whether a neuron should be activated or not.
- Whether the information that the neuron is receiving is relevant for the given information or should it be ignored.
- It is the non linear transformation that we do over the input signal.
- This transformed output is then send to the next layer of neurons as input.
What if we don’t have activation functions?
- Without activation function neural network will only be performing linear transformation on the input.
- A linear equation is simple to solve but is limited in its capacity to solve complex problems. A neural network without an activation function is essentially just a linear regression model.
- The activation function does the non-linear transformation to the input making it capable to learn and perform more complex tasks.
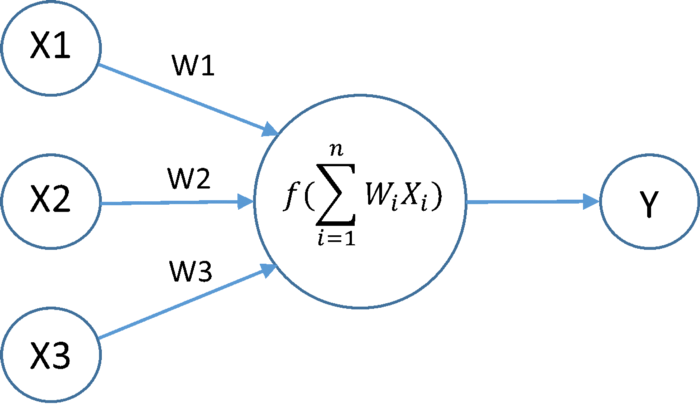
We would want our neural networks to work on complicated tasks like language translations and image classifications.
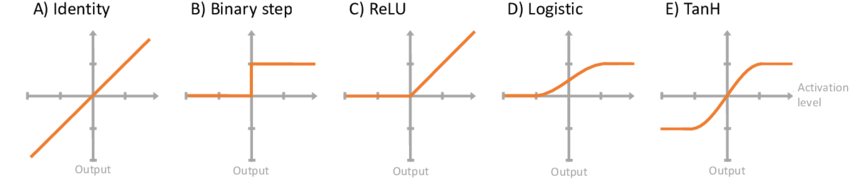
There are 3 types of Activations Functions:
- Binary Step Function
- Linear Activation Function
- Non-Linear Activation Function
Binary Step Function
It depends on a threshold value that decides whether a neuron should be activated or not. Whatever input we pass to the activation function is compared with certain threshold, if the input is greater than it, then the neuron is activated else it deactivated. It means that output is not being passed to the next layer.
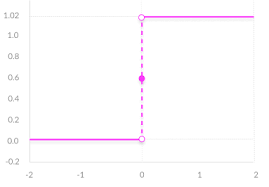
Mathematically it is represented as:

Disadvantages of Using Binary Step Function
- We cannot solve multi-classification problems
- The gradient of the step function is zero. This makes the step function not so useful since during back-propagation when the gradients of the activation functions are sent for error calculations to improve and optimize the results.
Linear Activation Function / Identity Function / No Activation Function
A straight line function where activation is proportional to input (which is the weighted sum from neuron).
This way, it gives a range of activations, so it is not binary activation. We can definitely connect a few neurons together and if more than 1 fires, we could take the max and decide based on that. So that is ok too. Then what is the problem with this?
If you are familiar with gradient descent for training, you would notice that for this function, derivative is a constant.
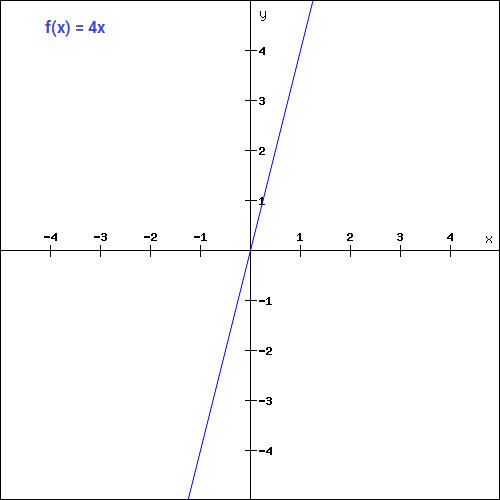
f = cx, derivative with respect to x is c.
That means, the gradient has no relationship with X. It is a constant gradient and the descent is going to be on constant gradient. If there is an error in prediction, the changes made by back propagation is constant and not depending on the change in input delta(x).
Disadvantages of Using Linear Activation Function
- Here the backpropagation is not possible because the derivative of the function is a constant and has no relation to the input x.
- We won’t be able to solve classification problems using linear activation function
Non-Linear Activation Function
Already discussed above the drawback of using linear activation function. Non-Linear activation functions solve the complex problems like multi-classification where we can have any number of categories in target variable. We can stack multiple layers of neurons together.
Sigmoid Activation Function
It is a activation function of form f(x) = 1 / 1 + exp(-x) . Its Range is between 0 and 1 and it's a S — shaped curve.
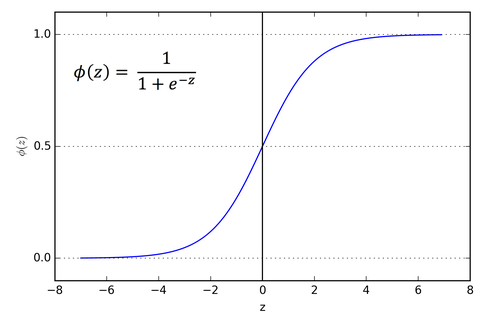
Mathematically it is represented as:
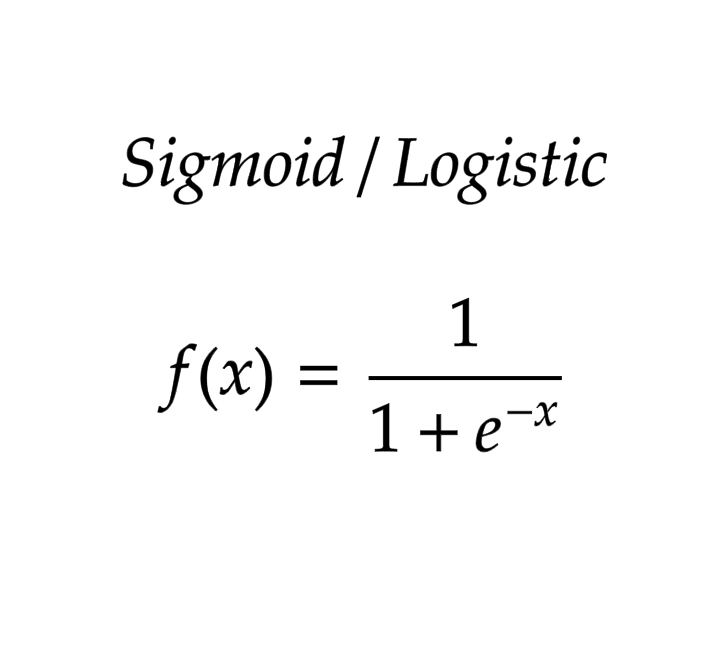
- It is easy to understand and apply but it has major reasons which have made it fall out of popularity - Vanishing gradient problem
- Secondly, its output isn’t zero centered. It makes the gradient updates go too far in different directions. 0 < output < 1, and it makes optimization harder.
- Sigmoid saturate and kill gradients.
- Sigmoid have slow convergence.
Tanh - Hyperbolic Tangent
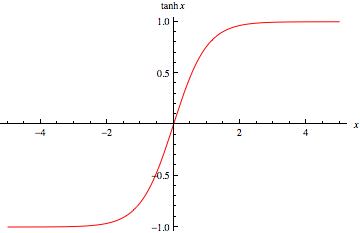
It’s mathematical formula is:
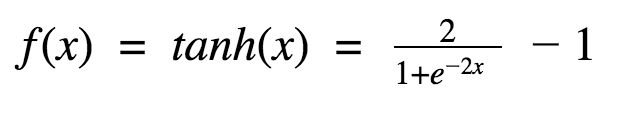
This looks very similar to sigmoid. In fact, it is a scaled sigmoid function!
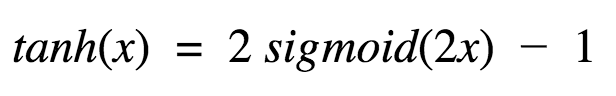
Now it’s output is zero centered because its range in between -1 to 1 i.e., -1 < output < 1 . Hence optimization is easier in this method hence in practice it is always preferred over Sigmoid function.
- It is nonlinear in nature,
- It is bound to range (-1, 1) so no worries of activations blowing up.
- One point to mention is that the gradient is stronger for tanh than sigmoid ( derivatives are steeper).
- Deciding between the sigmoid or tanh will depend on your requirement of gradient strength. Like sigmoid, tanh also has the vanishing gradient problem.
Softmax Function
What if we have to handle multiple classes ?
- The softmax function is also a type of sigmoid function but is handy when we are trying to handle classification problems.
- The sigmoid function as we saw earlier was able to handle just two classes. What shall we do when we are trying to handle multiple class? Just classifying yes or no for a single class would not help then.
- The softmax function would squeeze the outputs for each class between 0 and 1 and would also divide by the sum of the outputs. This essentially gives the probability of the input being in a particular class.
In mathematics, the softmax function (normalized exponential function) is a generalization of the logistic function
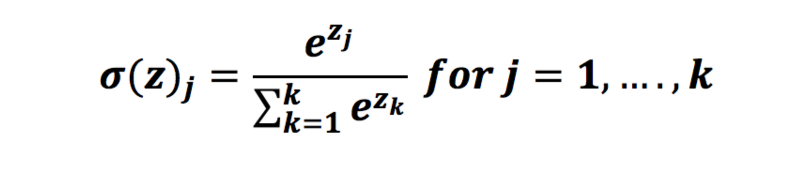
- transforms the values in the range [0,1] that add up to 1
- the softmax function is used in various multiclass classification methods
For example: when we classify handwritten digits ...
We use the softmax activation function in the last layer because we want to classify handwritten digits, we choose the class with the highest probability
ReLU Function
ReLU – Rectified Linear Unit
It is the most widely used activation function. It is defined as - R(x) = max(0,x)
- the ReLU function is non linear, which means we can easily backpropagate the errors and have multiple layers of neurons being activated by the ReLU function.
- It gives an output x if x is positive and 0 otherwise.
- It was recently proved that it had 6 times improvement in convergence from Tanh function. It’s just R(x) = max(0,x)
- if x < 0 , R(x) = 0 and if x >= 0 , R(x) = x.
- Hence as seeing the mathematical form of this function we can see that it is very simple and efficient. Also it avoids and rectifies vanishing gradient problem.
- The main advantage of using the ReLU function over other activation functions is that it does not activate all the neurons at the same time.
- If you look at the ReLU function if the input is negative it will convert it to zero and the neuron does not get activated.
- This means that at a time only a few neurons are activated making the network sparse making it efficient and easy for computation.
- ReLU is less computationally expensive than tanh and sigmoid because it involves simpler mathematical operations.

Disadvantages of ReLU
- Problem with ReLu - is that some gradients can be fragile during training and can die. It can cause a weight update which will makes it never activate on any data point again. Simply saying that ReLu could result in Dead Neurons.
- Because of the horizontal line in ReLu( for negative X ), the gradient can go towards 0. For activations in that region of ReLu, gradient will be 0 because of which the weights will not get adjusted during descent.
- That means, those neurons which go into that state will stop responding to variations in error/ input ( simply because gradient is 0, nothing changes ). This is called dying ReLu problem.
- This problem can cause several neurons to just die and not respond making a substantial part of the network passive.
- There are variations in ReLu to mitigate this issue by simply making the horizontal line into non-horizontal component.
- for example y = 0.01x for x<0 will make it a slightly inclined line rather than horizontal line. This is leaky ReLu.
- There are other variations too. The main idea is to let the gradient be non zero and recover during training eventually.
Leaky ReLU
Leaky ReLU function is nothing but an improved version of the ReLU function to solve dying ReLU problem.

What we have done here is that we have simply replaced the horizontal line with a non-zero, non-horizontal line. Here a is a small value like 0.01 or so. It can be represented on the graph as-
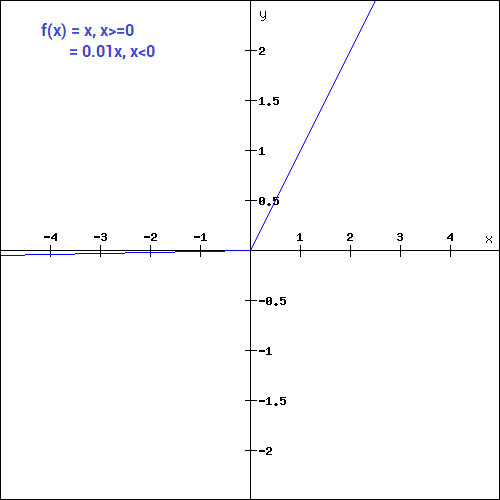
Disadvantages of Leaky ReLU
Predictions may not be consistent for negative values
Parametric ReLU Function
Parametric ReLU is another variant of ReLU that is used to solve the problem of gradient’s becoming zero for the left half of the axis. Parametric ReLU introduces a new parameter that is slope of the negative part of the function.
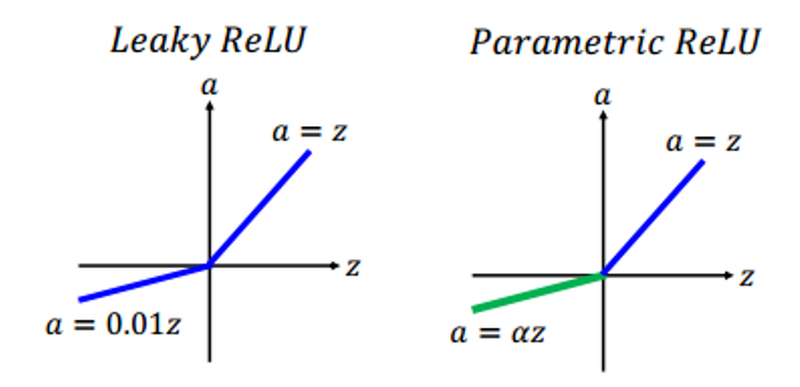
Mathematically it is written as
F(x) = max(ax, x)
Where a is the slope parameter for negative values. If we set value of a = 0.01, the function acts as a Leaky ReLU function. But here ‘a’ is a trainable parameter. We can make our model learn the value of ‘a’ as well.
Disadvantages of Parametric ReLU
It may perform differently for different problems depending upon the value of slope parameter a
ELU Activation Function
ELU – Exponential Linear Units
Another variant of ReLU is ELU that modifies the slope of negative part of the function. Instead of a straight line ELU uses a log curve to define the negative values

Mathematically it is represented as
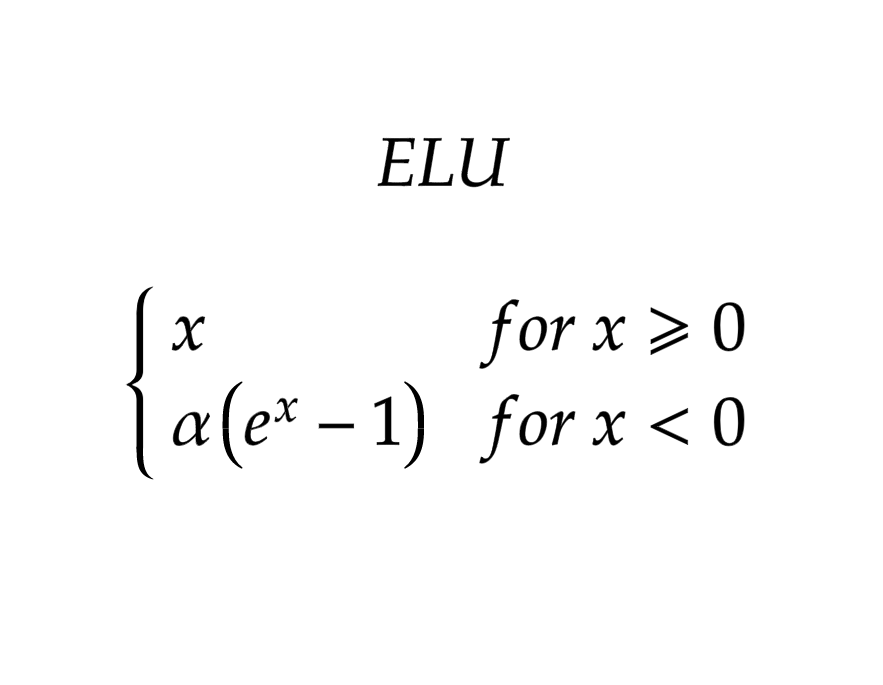
ELU helps to avoid dead ReLU problem by introducing log curve for negative values of input
Disadvantages of ELU
- It may increase the computational time because of exponential operation performed
- No learning of ‘a’ takes place
- It may explode gradient
Swish Activation Function
One of the underrated activation function is Swish that was discovered by researchers at Google. Swish is computationally efficient just like ReLU on deep networks. Value for swish range is from (-)ve infinity to (+)ve infinity

Mathematically it is represented as

It may outperform ReLU because we can see in above graph the curve of the function is smooth. It doesn’t change direction like ReLU does near x = 0. It smoothly handles the values as it bends from 0 towards values & 0 and then upwards again. This is helpful in model optimization process. Another benefit of using Swish is that it is not monotonic which means the value of the function may decrease even when the input values are increasing.
GELU
GELU - Gaussian Error Linear Unit
It is mostly compatible with models like BERT, ALBERT, ROBERTa and other NLP models. It combines the properties from dropout, zoneout and ReLU.

Mathematically it is represented as:
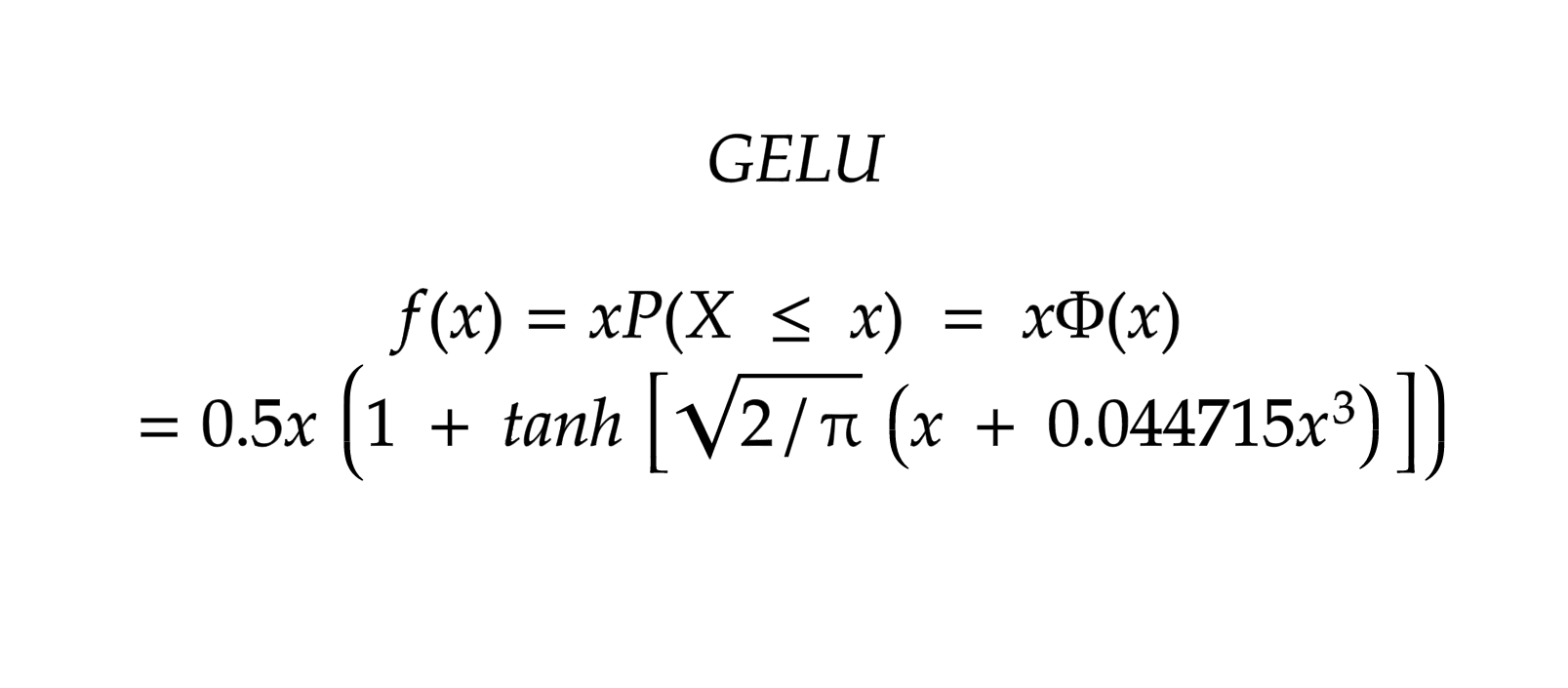
GELU nonlinearity is better than ReLU and ELU activation functions.
SELU
SELU – Scaled Exponential Linear Unit
SELU was introduced in self-normalizing networks and takes care of internal normalization which means each layer preserves the mean and variance from the previous layer. SELU enables this normalization by adjusting mean and variance.
ReLU activation cannot adjust the negative values but SELU has both positive and negative values to shift the mean.
Mathematically SELU is represented as

SELU has values of alpha α and lambda λ predefined.
SELU is one of the latest activation functions that could be used more in research and academics.
You can find python implementation of all activation functions here
That’s all for this blog.
