
What we are gonna learn?
- What is a Loss Function ?
-
Types of Loss Functions
- Regression Loss Functions
- Binary Classification Loss Functions
- Multi-Class Classification Loss Functions
-
Regression Loss Functions
- Mean Squared Error
- Mean Squared Logarithmic Error Loss
- Mean Absolute Error
- Huber Loss
-
Binary Classification Loss Functions
- Binary Cross Entropy
- Hinge Loss
- Squared Hinge Loss
-
Multi-Class Classification Loss Functions
- Multi-Class Cross Entropy Loss
- Sparse Multi-Class Cross Entropy Loss
- Kulback Liebler Divergence Loss
What is a Loss Function ?
When we start with feedforward in neural network then we initialize weights randomly and if the weights are initialized randomly then obviously the predictions will alse be random.
That's why we need to optimize the model to make our model better and update weights and biases in each iteration to get better prediction. But how do we know that our model is optimized...??????
That's where comes the need of Loss Functions which will help us to find out the amount of loss we are having while training the model.
Loss function is a method through which we judge our model that how well it is fitted with our dataset. Because it tells the difference between the actual and predicted value.
"The better the model is less the loss will be"
1. Regression Loss Functions
Regression models deals with situations where the type of target column is continuous like predicting a quantity or something. For example stock market of tomorrow or upcoming days, tomorrow's temprature or any other numeric continuous data.
1.1 Mean Squared Error
One of the most popular and commonly used loss function is mean squared error. Where we find out average difference by actual and predicted values.
Mathematically MSE is represented as :
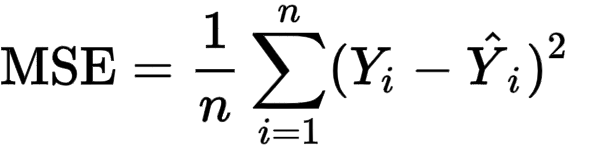
There is another version of MSE that is RMSE - Root Mean Squared Error
In RMSE we simply do the square root of MSE.
Mathematically MSE is represented as :

1.2 Mean Squared Logarithmic Loss Function
There might be situations in regression problems in which the target value has a spread of values and when predicting a large value you may not want to punish a model as heavily as MSE.
Instead you can first calculate the natural logarithmic of each of predicted value then calculate MSE. This is called as Mean Squared Logarithmic Loss. MSLE is the relative difference between the log-transformed actual and predicted values.
Mathematically it is represented as :
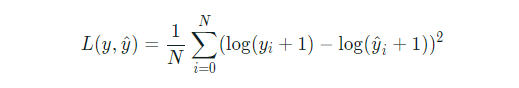
where ŷ is the predicted value.
This can also be interpreted as the ratio between true and predicted values and can be written as:
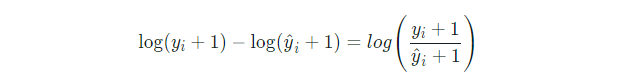
1.3 Mean Absolute Error
MAE is one of the popular loss function used for regression models.
It measures the average magnitude of errors in a group of predictions, without considering their directions.
Regression problems may have variables that are not strictly Gaussian in nature due to the presence of outliers. Mean Absolute Error would be an ideal option in such cases because it does not take into account the direction of the outliers.
Mathematically it is represented as:

1.4 Huber Loss
Huber loss is another kind of loss function we use for regression problems. Huber loss is less sensitive to outliers.
It is defined as the combination of MSE and MAE loss functions because it approaches MSE when 𝛿 ~ 0 and MAE when 𝛿 ~ ∞ (large numbers).
It is quadratic for smaller errors and is linear otherwise. To make the error quadratic depends on how small that error could be, which is controlled by a hyperparameter, 𝛿 (delta) that you can tune.
Mathematically it is represented as :
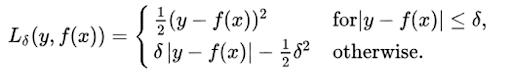
Therefore, you can use the Huber loss function if the data is prone to outliers. In addition, we might need to train hyperparameter delta, which is an iterative process.
2. Binary Classification Loss Functions
Binary Classification Loss Functions are used in binary classification problems where the target variable is either 0 or 1. For example win or loss, diseased or not diseased etc.
2.1 Binary Cross Entropy Loss Function
This is one of the most common loss function used in classification problems. Binary cross entropy measures how far away the true value the prediction is for each class and then average these class-wise errors to obtain final loss.
It measures performance of a classification model whose predicted output is a probability value between 0 and 1.
Mathematically it is represented as:

2.2 Hinge Loss Function
The another popular loss function for binary classification is Hinge Loss and it is an alternative to the cross entropy function. Hinge Loss is primarily used for "maximum-margin" classification, most notably for SVM.
It is represented mathematically as:
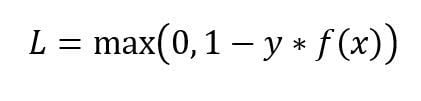
2.3 Squared Hinge Loss Function
Hingle Loss has many extensions. One of the popular extension is called as Squared Hinge Loss where we simply calculate the square of the hinge loss.
It is used in binary classification problems and when you're not interested in knowing how certain the classifier is about the classification (i.e., when you don't care about the classification probabilities). Use in combination with the tanh() activation function in the last layer.
It is mathematically represented as:
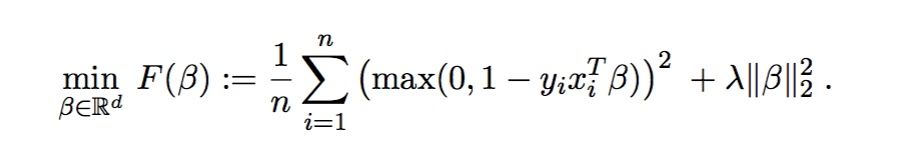
3. Multi-Class Classification Loss Functions
Multi-Class Classification Loss Functions will be used when the target column will have more than 2 classes. We can use these functions in problems like classifying hand written digits where we have 10 categories to classify.
3.1 Multi-Class Cross Entropy Loss
Most of the times Multi-Class Cross Entropy Loss is used as a loss function. The generalised form of cross entropy loss is the multi-class cross entropy loss.
Mathematically it is represented as :

Categorical Cross Entropy Loss
Also called as Softmax Loss. It is a Softmax activation plus a Cross-Entropy loss. If we use this loss, we will train our model to output a probability over the n classes for each image. It is used for multi-class classification.

3.2 Sparse MultiClass Cross Entropy Loss
One of the main problem while using cross-entropy with classification problems with a large number of labels is the one hot encoding process.
For example, predicting words in a vocabulary may have tens or hundreds of thousands of categories, one for each label. This can mean that the target element of each training example may require a one hot encoded vector with tens or hundreds of thousands of zero values, requiring significant memory.
Sparse cross-entropy addresses this by performing the same cross-entropy calculation of error, without requiring that the target variable be one hot encoded prior to training.
Kullback-Liebler Divergence Loss
KL Divergence is a measure of how a probability of one distribution is different from another distribution.
The behavior of KL Divergence is very similar to cross-entropy. It calculates how much information is lost if the predicted probability distribution is used to approximate the desired target probability distribution
Dkl(P||Q) is interpreted as the information gain when distribution Q is used instead of distribution P.
Dkl(Q||P) is interpreted as the information gain when distribution P is used instead of distribution Q.
Information gain (IG) measures how much “information” a feature gives us about the class.
Mathematically it is represented as:
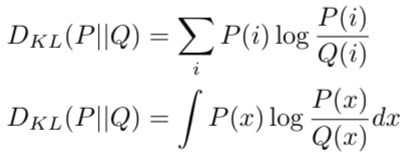
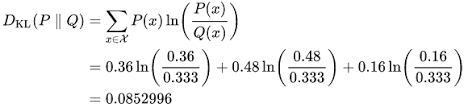
Here the goal of the KL divergence loss is to approximate the true probability distribution P of our target variables with respect to the input features, given some approximate distribution Q. This Can be achieved by minimizing the Dkl(P||Q) then it is called forward KL. If we are minimizing Dkl(Q||P) then it is called backward KL.
Conclusion
In this blog we have covered few popular loss functions that we use in deep learning. Picking a loss function is not a big task if we are using tensorflow or pytorch or any other framework. We don't have to implement the mathematical part of any of the loss function. But it's necessary to know about how they work.
