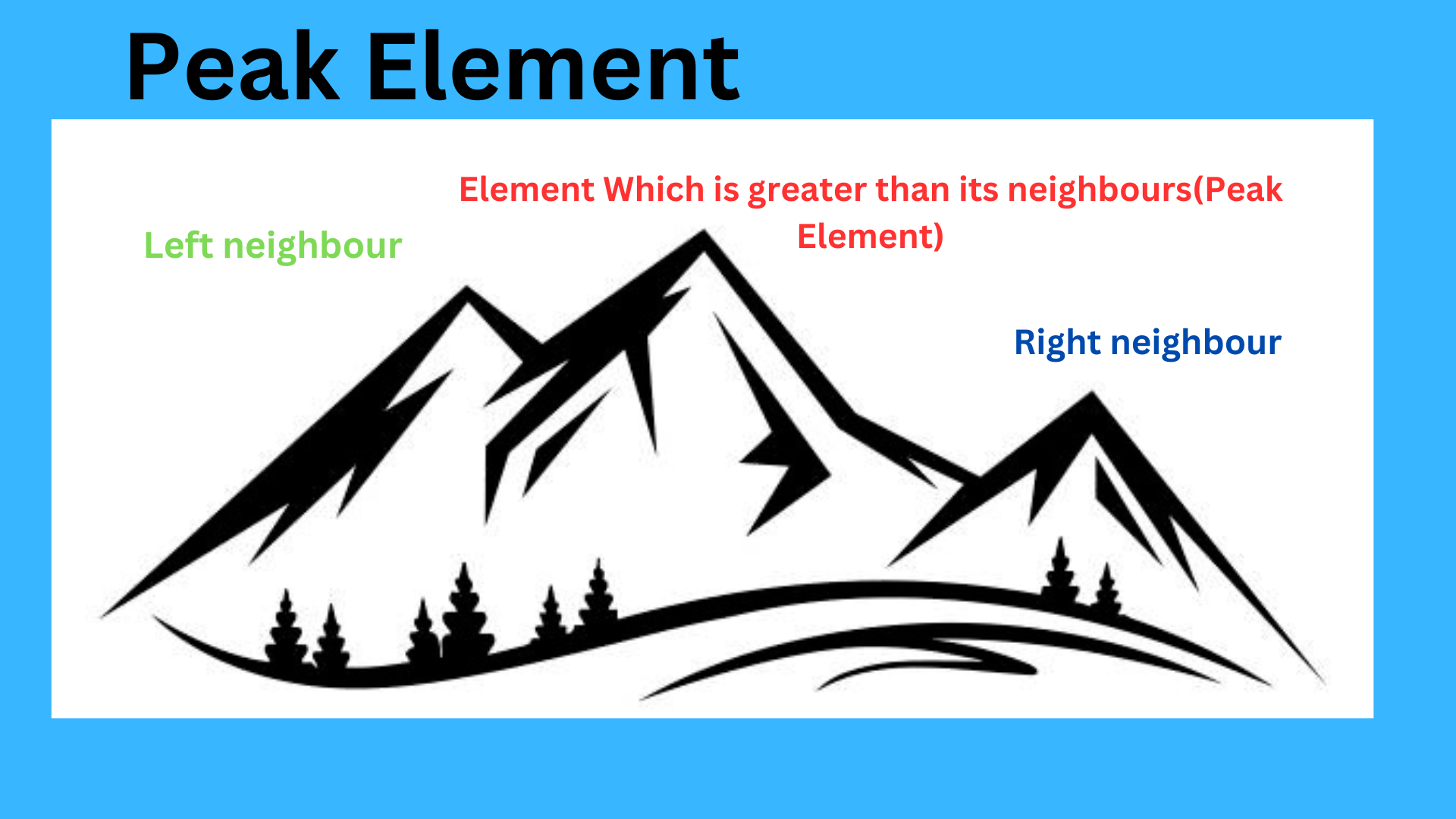
Peak element is the element which have greater value then their neighbours value.

Example:
Input: array[] = {60,10,55,12,46,86,31}
Output: 55 or 86
Explanation: The element 55 has neighbors 10 and 12 both of them are less than 55, similarly 86 has neighbors 46 and 31.

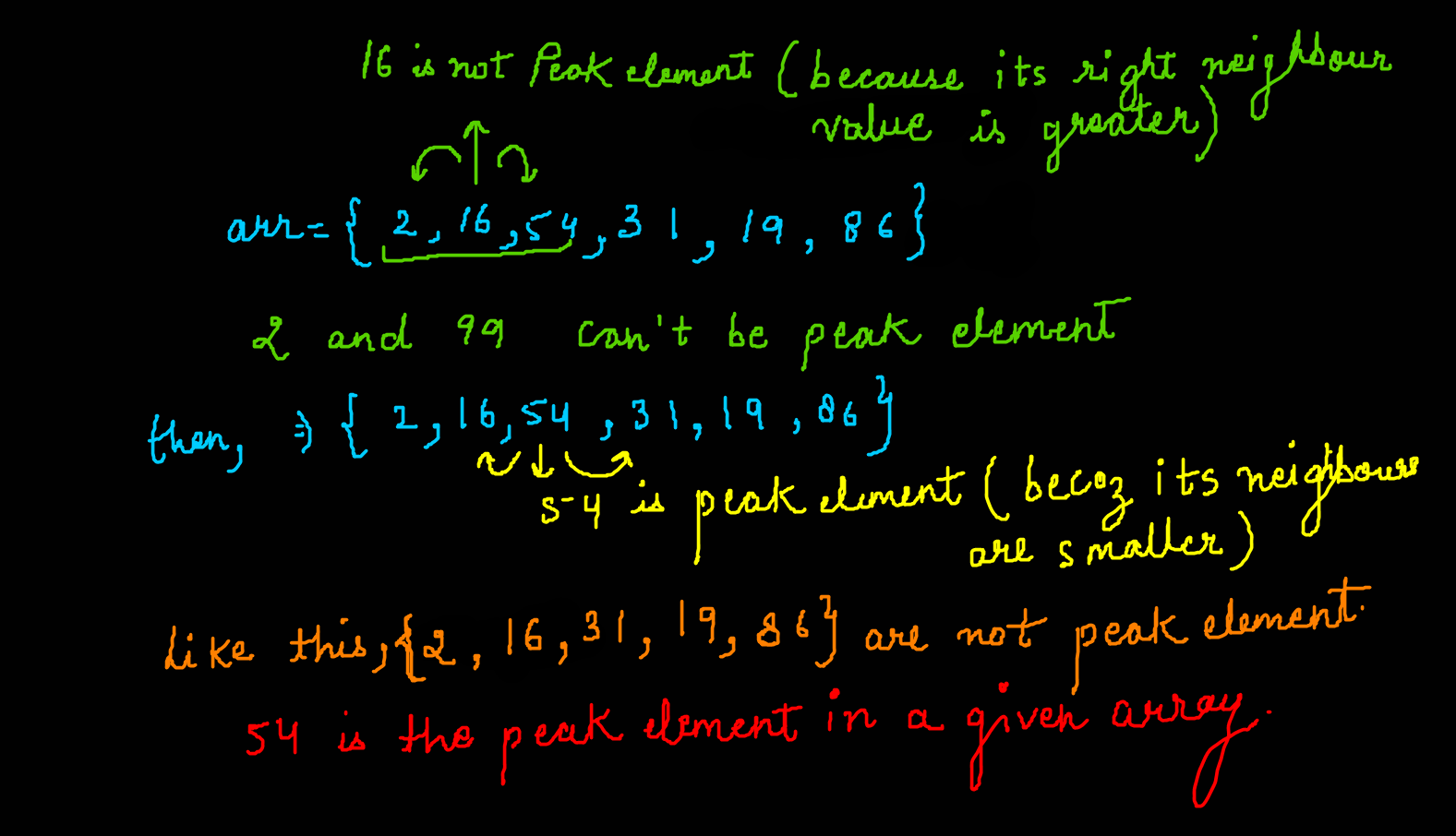
Method 1:

We can solve this problem by using Linear Search algorithm:

There are following steps to implement this approach:

1. Traverse the array from the second index to the
   second last index i.e. 1 to N – 1.( Note:- first and last element can't be peak because they don't have both left and right neighbour).
2. If an element array[i] is greater than both its neighbours,
   i.e., array[i] > =array[i-1]  and array[i] > =array[i+1] , then
   print that element and terminate.
3. If peak element not found ,then return -1.

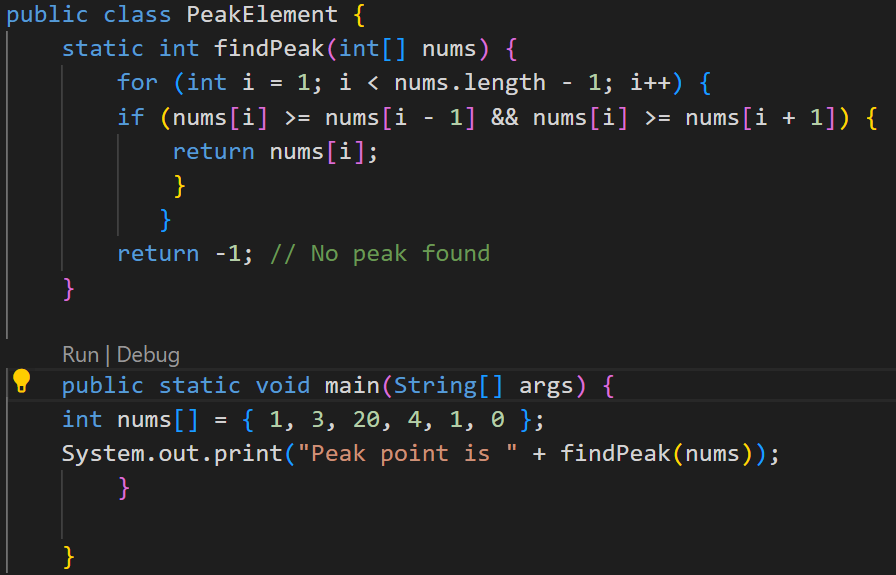
Output:-

Note :-Time Complexity of this approach is O(n), where n is the number of elements in the array.
This is the simplest approach to find the peak element but not the optimized.

Method 2:

We can also solve this problem by using Binary Search algorithm:

There are following steps to implement this approach:

1.Let's create two variables low and high with initailization of 0 and n(Size of an array)-1 respectively.

2. Then , find the index for middle element ,mid = low + (high – low) / 2.

3. Compare middle element with its neighbours ,if there is middle element is peak or not,if it is then print the output .

4. If middle element is not a peak element and its left element is greater, then check on the left side for finding the peak element,(Perform recursive calls)update the parameter's value of high (mid -1 ).

5.If left sided elements are not the peak element and its right element is greater, then check on the right side for finding the peak element,(Perform recursive calls)update the parameter's value of low (mid +1 ).

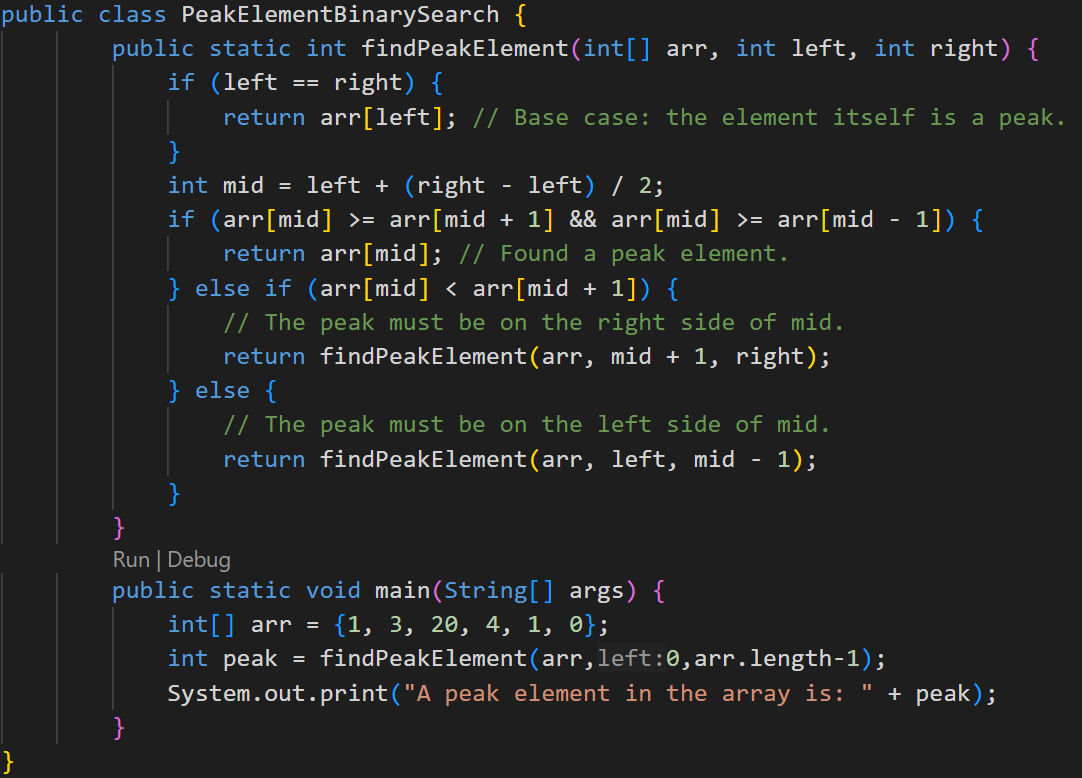
output:

Note :-Time Complexity of this approach is O(log n), where n is the number of elements in the array.

It is the optimized approach for solving this problem.