Given a Big String and we need to lookup the small string from the big string. eg. String str = “ABCABCD” String pattern = “ABC” output : 0 3 e.g String str = “AAAAA” String pattern “AAA” output 0 1 2
use cases : google search , shopping search
There are some popular algo for pattern matching a) Naive Pattern Matching Algo b) Rabin Karp c) KMP
Naive pattern searching is based on sliding technique it slide the pattern in given string.
// Use Sliding Technique
static void naivePatternSearchingAlgo(){
String str = "ABABABCD";
String pattern ="ABAB";
int patternLen = pattern.length();
for(int i = 0; i<str.length()-patternLen; i++){
int j;
for( j = 0; j<patternLen; j++){
if(pattern.charAt(j)!=str.charAt(i+j)){
break;
}
}
if(j==patternLen){
System.out.println("Pattern Found "+i);
return;
}
}
System.out.println("No Pattern");
}
TC O (N-M+1) * M
It is not best algo for pattern matching as it is quadric time taking
Improve Naive Algo for Distinct Character in the pattern e.g str = “ABCABCDABCD” pattern = “ABCD” output 3 , 7 e.g str = “ABCAAAD”; pattern = “ABD” output : -1
class NaivePatternForDistinctChar{
public static void main(String[] args) {
String str = "ABCABCD";
String pattern = "ABCD";
int n = str.length();
int p= pattern.length();
for(int i = 0; i<=n-p; ){
int j;
for(j = 0; j<p; j++){
if(pattern.charAt(j)!=str.charAt(i+j)){
break;
}
}
if(j==p){
System.out.println("Pattern found "+i);
}
if(j==0){
i++;
}
else{
i = (i+j); // Jump to start of next pattern
}
}
}
}
Rabin Karp Algorithm
Naive Algorithm has Quadric Time Complexity, where Rabin Karp also has Quadric Time Complexity in worst case but in average case it works better
pattern = “bbb” bbb present at 0 1 and 2 index example: text = “abcdefg” pattern = “pqr” Not found any pattern

Note : For this approach we save lot of bigger comparison , might be there hashcode are not same , so they never compare the chars.

We need to create the Rolling Hash, Remove the Slide first Char and Add the Last Char of the Slide.
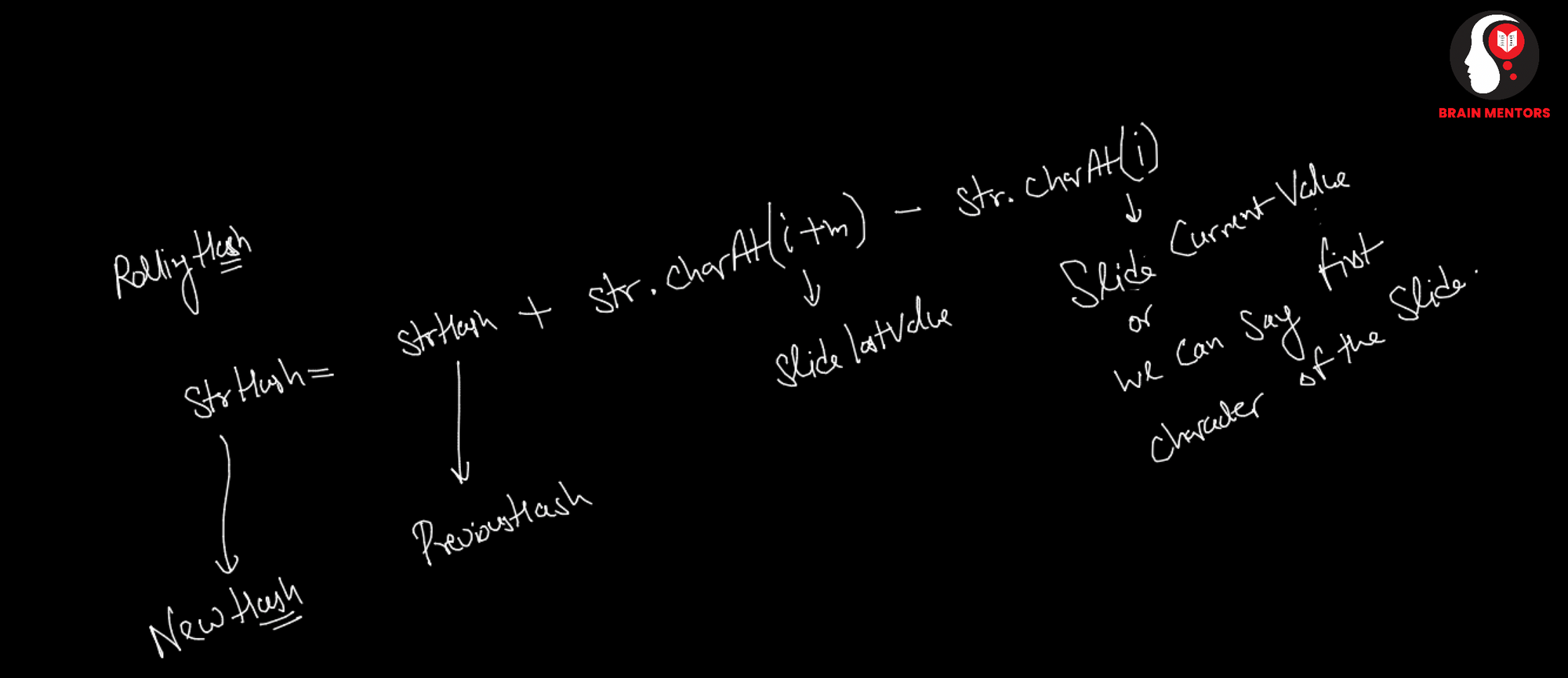
So Rolling Hash can be computed O(1) Due to the above formula.
Now also we need to treat the Spurious Hit, where abc and bac and cab has the same Hash value , so to solve this problem. If u have the many permutations of the same string so u have many Spurious Hit
To Solve this issue instead of doing simple ascii sum we do the weighted sum.

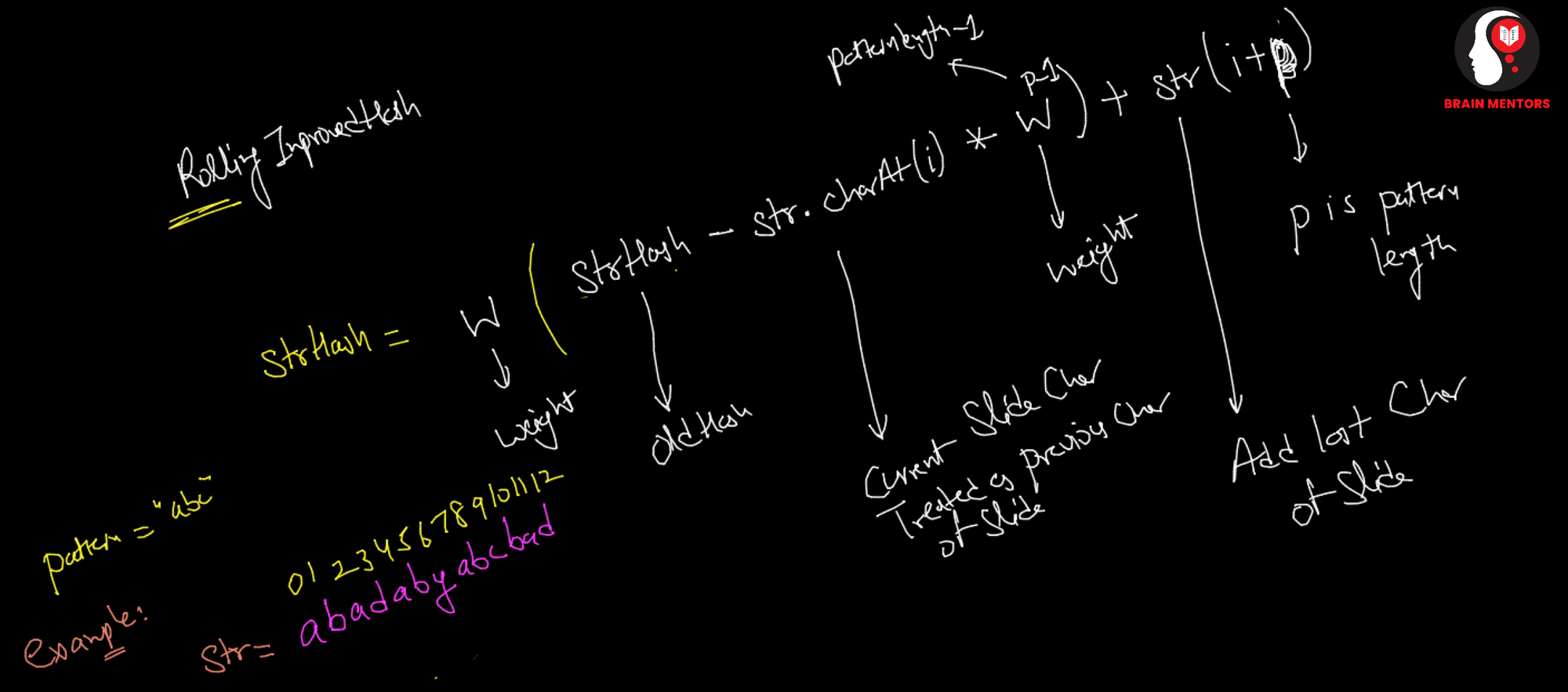

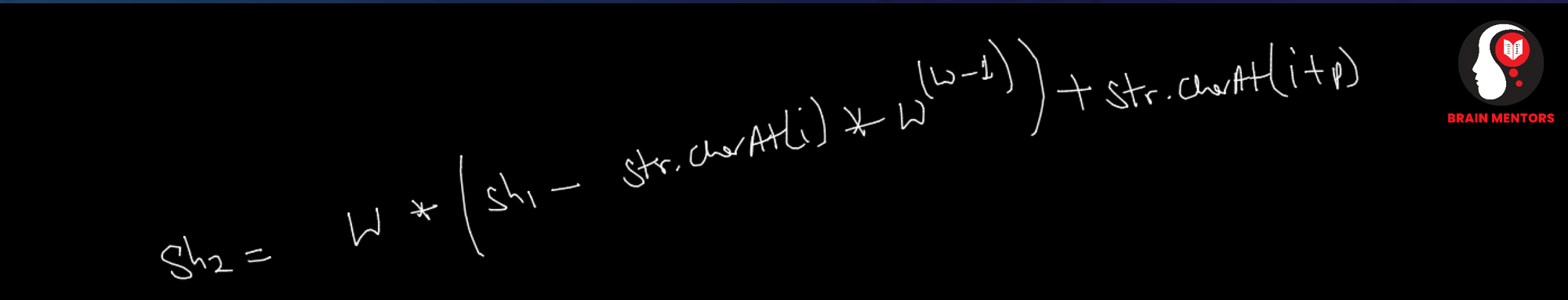

ArrayList<Integer> robinKarp(String pattern, String str)
{
ArrayList<Integer> list = new ArrayList<>();
int n = str.length();
int p = pattern.length();
int d = pattern.length();
int x = 1;
// int d = 256;
int q = 13;
int stringHash = 0;
int patternHash = 0;
for(int i = 0; i < p-1; i++) {
x = (x * d) % q;
}
for(int i = 0; i < p; i++) {
patternHash = (patternHash * d + (pattern.charAt(i))) % q;
stringHash = (stringHash * d + str.charAt(i)) % q;
}
for(int i = 0; i <= n - p; i++) {
if(patternHash == stringHash) {
int j = 0;
for(j = 0; j < p; j++) {
if(pattern.charAt(j) != str.charAt(i + j)) {
break;
}
}
if(j == p) {
list.add(i+1);
}
}
if(i < n - p) {
stringHash = stringHash - (str.charAt(i) * x);
stringHash = ((stringHash * d + str.charAt(i + p))) % q;
if(stringHash < 0) {
stringHash = stringHash + q;
}
}
}
if(list.size() ==0) {
list.add(-1);
}
return list;
// your code here
}
KMP Algo (Knuth–Morris–Pratt algorithm)
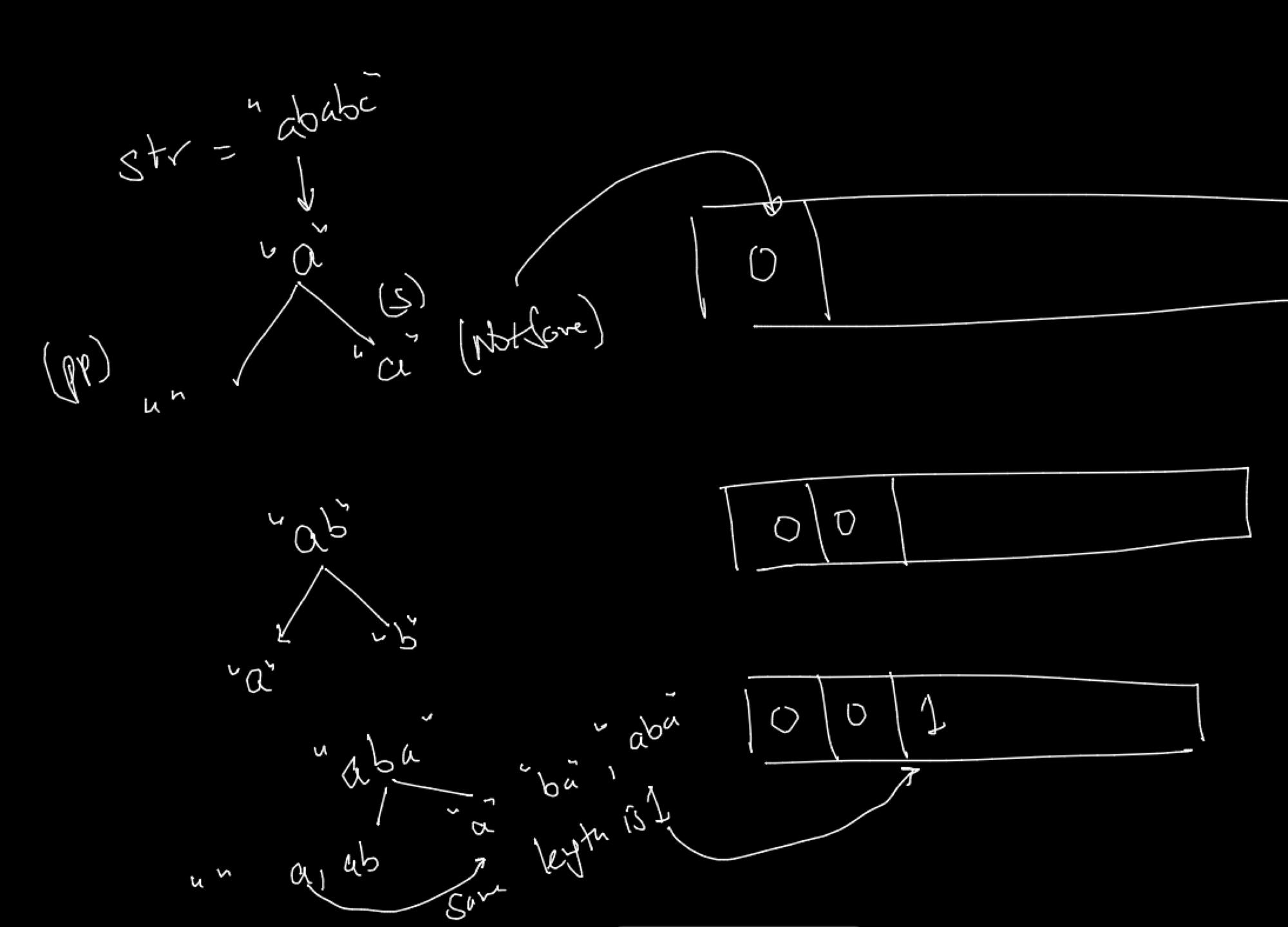
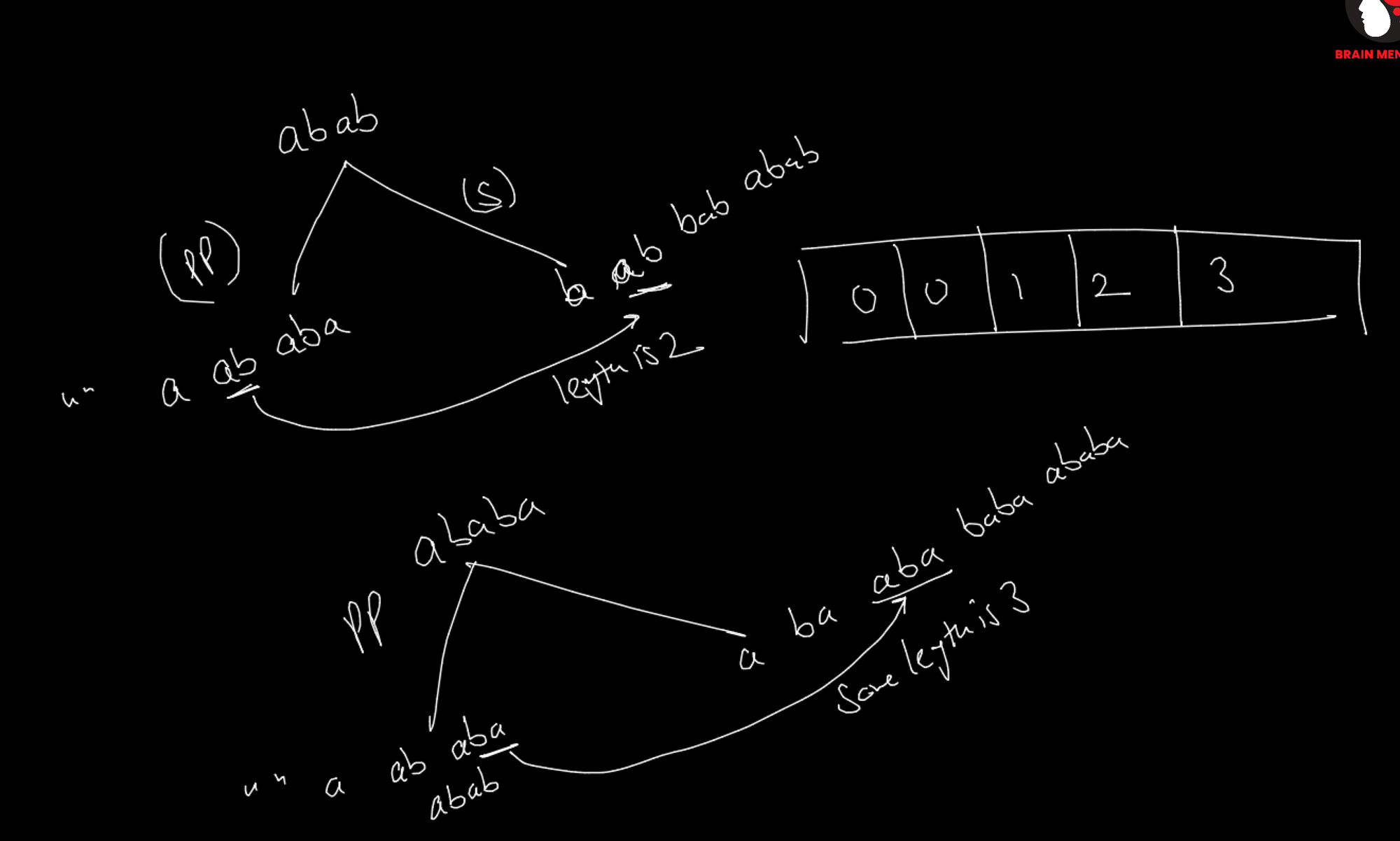
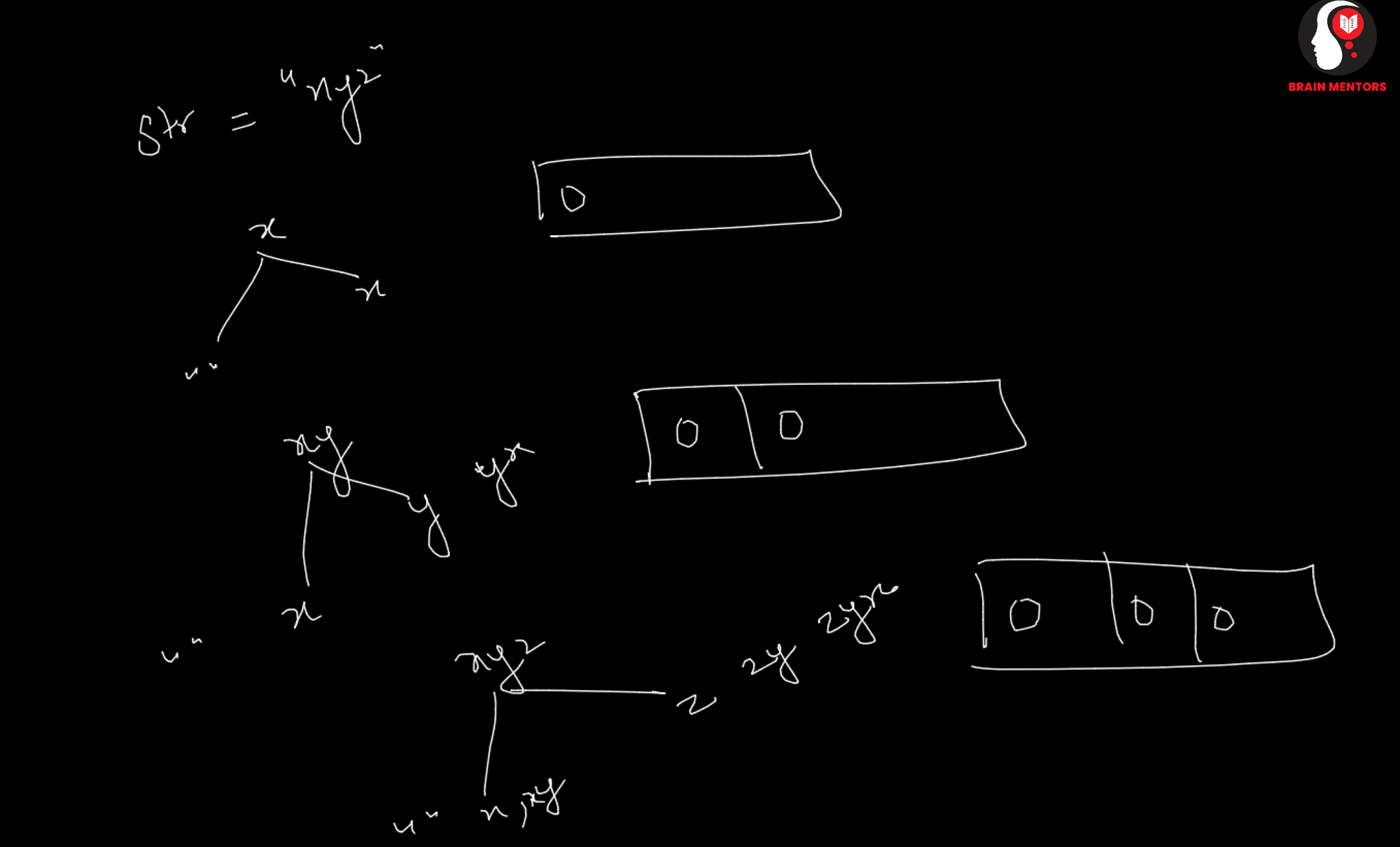
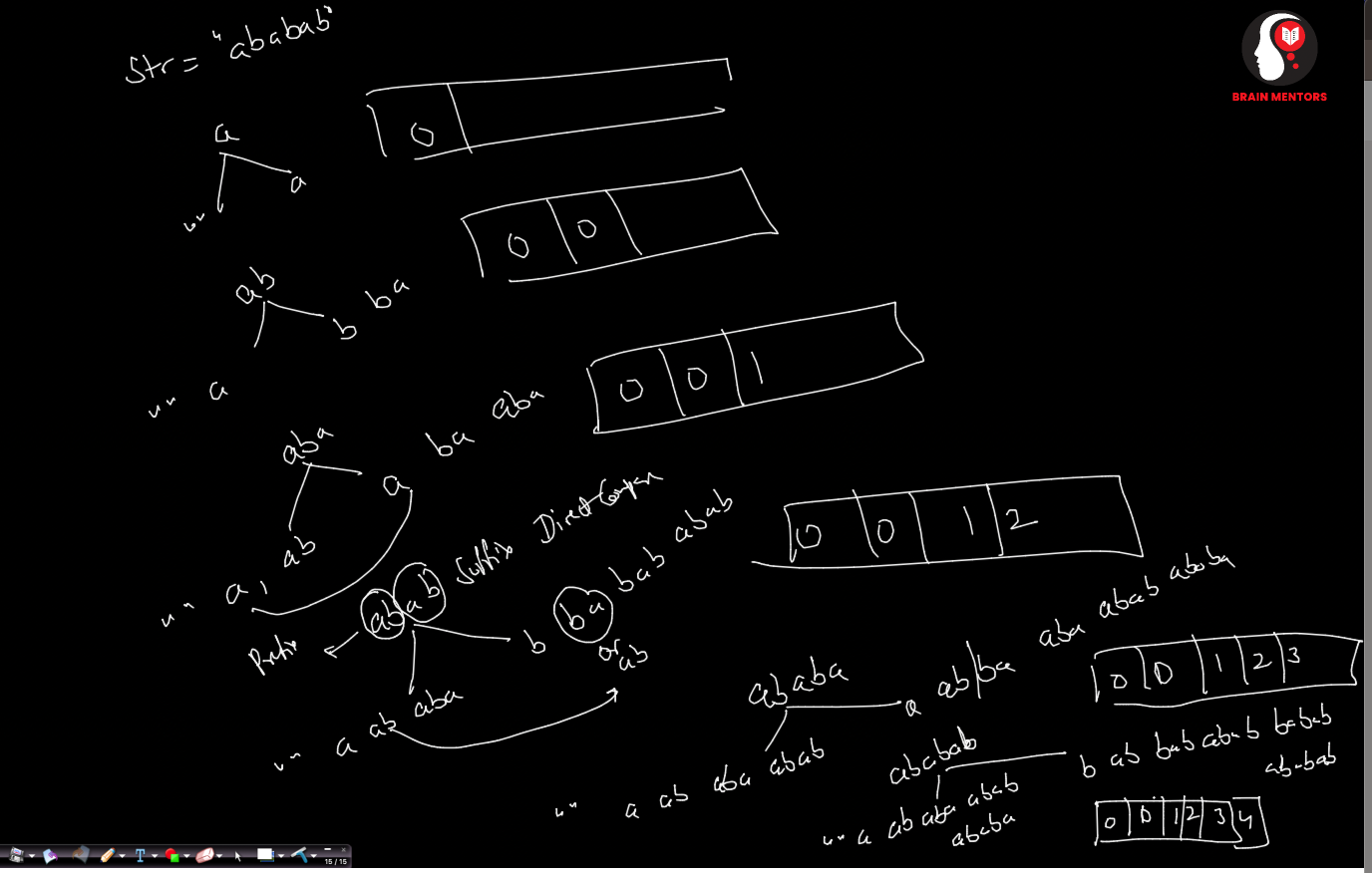
We need to first construct LPS (Longest Prefix and Suffix ) Array.
Proper Prefix of “abcd”
“” , “a” ,”ab”, “abc” (Note abcd not a proper prefix, the proper prefix length is smaller than the given string)
Suffix of “abcd”
“” “d” “cd” “bcd” , “abcd”
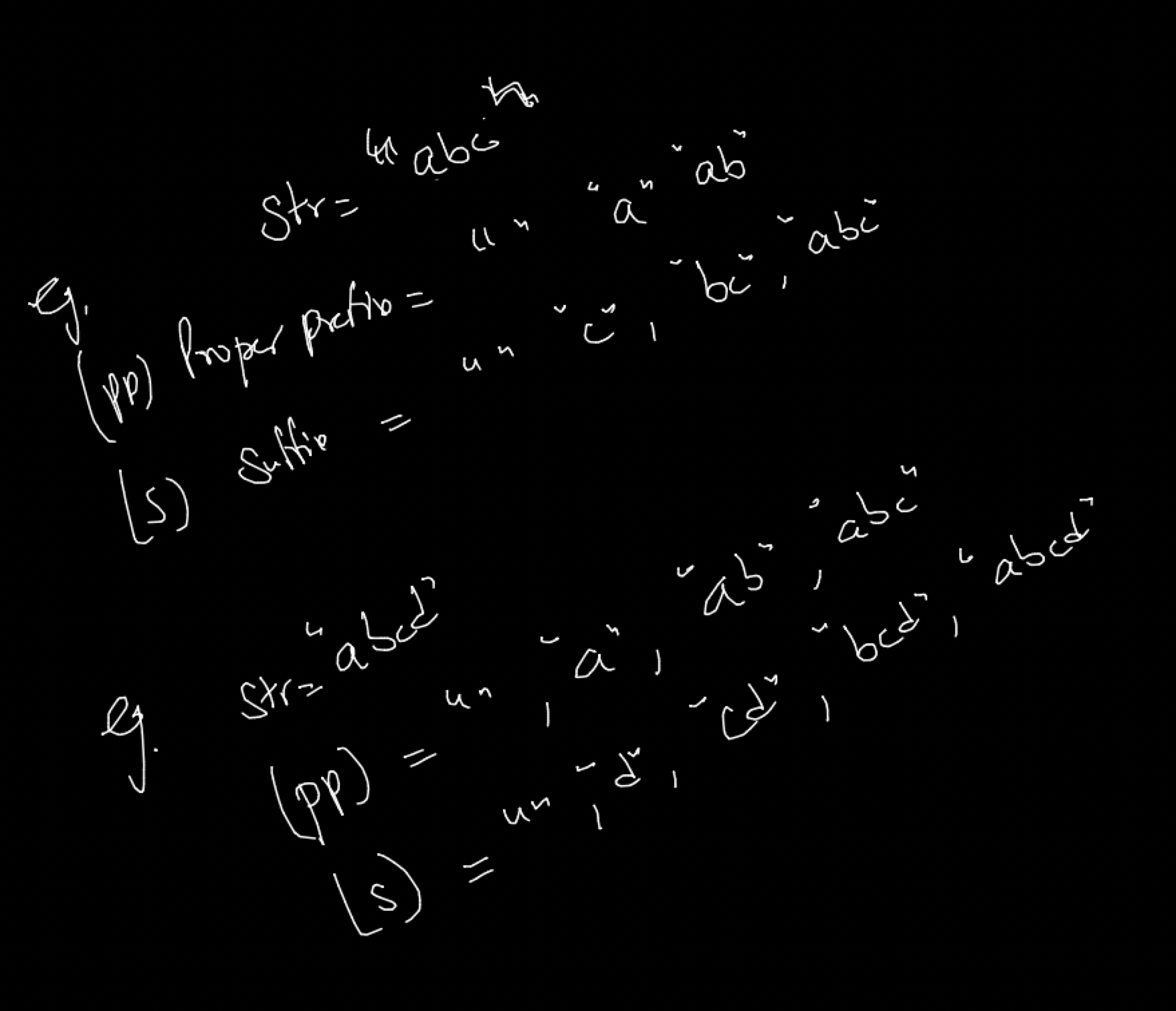

// KMP LPS Array Generation Code
public class KMP {
// KMP LPS Array Generate (O (N^3 ))
static int LPS(String str, int n){
for(int len = n-1; len>0; len--){
boolean isMatch = true;
for(int i = 0 ; i<len; i++){
if(str.charAt(i)!= str.charAt(n-len+i)){
isMatch = false;
}
}
if(isMatch){
return len;
}
}
return 0;
}
public static void main(String[] args) {
// Size of the LPS Array (Size of the str)
// Calling Slow Solution
String str = "ababc";
int lps [] = new int[str.length()]; // 0, 0, 1, 2, 0
for(int i = 0 ; i<str.length(); i++){
lps[i] = LPS(str, i+1);
System.out.print(lps[i] +" ");
}
System.out.println();
}
}
TC O(N^3)
Better Solution is
static void efficent(String str, int [] lps){
int n = str.length();
int len = 0;
lps[0] = 0; // because first prefix is blank so not match with suffix
int i = 1; // start from the 2nd Char (on 1st index)
while(i<n){
if(str.charAt(i)==str.charAt(len)){
len++;
lps[i] = len;
i++;
}
else {
if(len==0){
lps[i] = 0;
i++;
} else {
len = lps[len-1];
}
}
}
}
// Calling Code
// Calling Efficent way
String str = "ababc";
int lps [] = new int[str.length()]; // 0, 0, 1, 2, 0
efficent(str, lps);
for(int i : lps){
System.out.print(i+" ");
}
System.out.println();KMP Full Code
public class KMPFull {
static void efficent(String str, int [] lps){
int n = str.length();
int len = 0;
lps[0] = 0; // because first prefix is blank so not match with suffix
int i = 1; // start from the 2nd Char (on 1st index)
while(i<n){
if(str.charAt(i)==str.charAt(len)){
len++;
lps[i] = len;
i++;
}
else {
if(len==0){
lps[i] = 0;
i++;
} else {
len = lps[len-1];
}
}
}
}
public static void main(String[] args) {
String str = "abcabxabyabcabba";
String pattern = "abc";
int n = str.length();
int p = pattern.length();
int lps []= new int[pattern.length()];
efficent(pattern, lps);
int i = 0;
int j = 0;
while(i<n){
if(pattern.charAt(j)== str.charAt(i)){
i++; j++;
}
if(j==p){
System.out.println("Pattern Found "+(i-j));
j = lps[j-1];
}
else if(i<n && pattern.charAt(j)!= str.charAt(i)){
if(j==0){
i++;
}
else{
j = lps[j-1];
}
}
}
}
}
That's All Folks, Catch you in the next blog , Happy Coding :)
