Rotating an array by k positions in Java involves shifting the elements of an array to the right (or left) by a specified number of positions, k. This operation effectively reorders the elements in the array. The goal is to maintain the relative order of elements while moving the last k elements to the beginning (or the first n-k elements to the end).
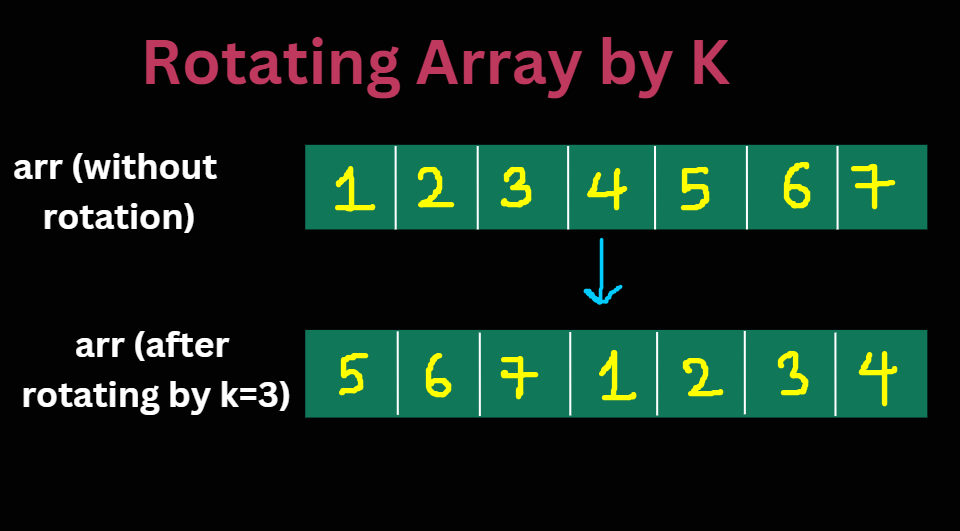
Example:Suppose you have an array [1, 2, 3, 4, 5, 6, 7] and you want to rotate it by `k = 23 positions to the right. The rotated array will be [ 5, 6, 7, 1, 2, 3, 4], where each element has shifted three positions to the right.
There are various methods to solve this problem .So,we look at the Simplest approach which uses the concept of looping.
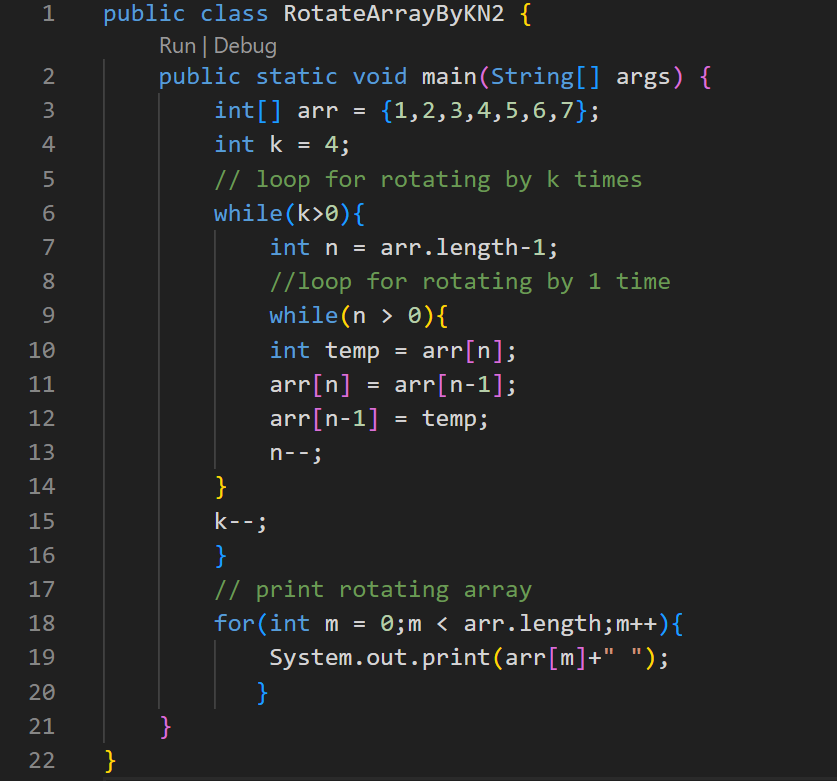
Method 1:Using loops
Step 1: Here ,we used two while loops. One loop is for rotating of an array by 1 time.
Second is for rotation of array by k times.
Step 2: print the array .
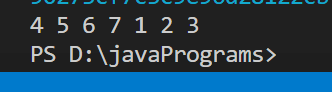
Output:
Explain:
Here is an array which is rotating by k.Outerloop dependent on the value of k ,if it is not equal to zero then it iterates.In this example,Value of k is 2.
So,the condition of outerloop will be true then ,the loop will iterate.

when outer loop is updated by k-1.Now, k = 1.

Now, K = 0 after the updation of k.So, the condition of outerloop will be false that's why further iterations don't take place.
The timeComplexity of this approach is O(k*n),where n is number of iterations which is done in swapping and "k" is the number of rotations.
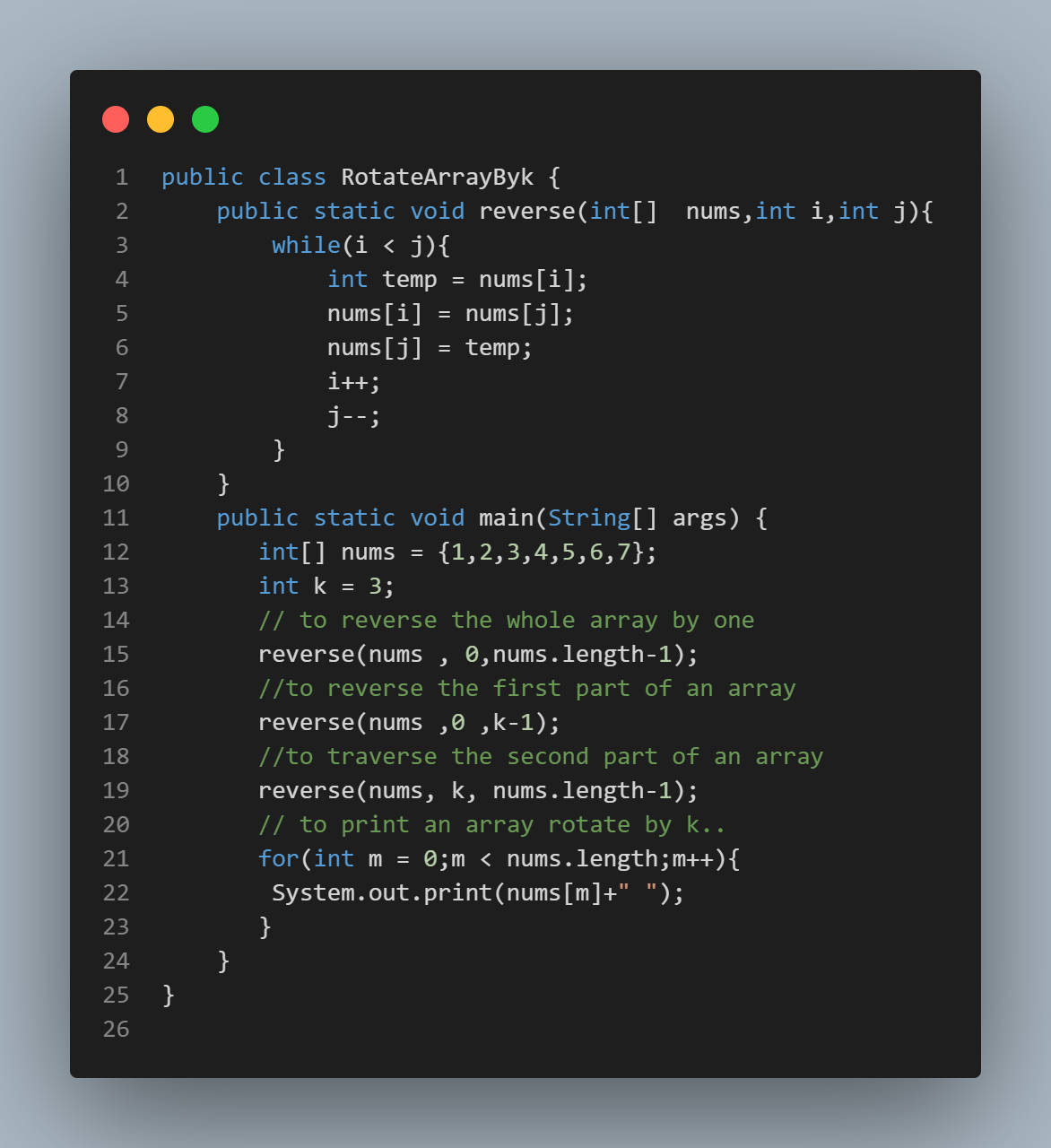
Method 2: Using Functions:
In this method, we use the reversing of an array and the reversing particular parts of an array.Here ,three functions are used to rotate an array by k times.
Step 1: In the First Reverse Function, we rotate the array by using the swapping concept(it reverse the whole array by 1 time).
Step 2:In the Second Reverse Function, we reverse the first part of an array.
Step 3:In the Third Reverse Function, we reverse the second part of an array.
Step 4:Print the rotating array.
Output:
The timeComplexity of this approach is O(n),where n is number of elements in an array.
