Tree Preorder Traversal Using Loops

We have Given a Tree and the task is to find the Preorder Traversal of that tree.

Example 1 :

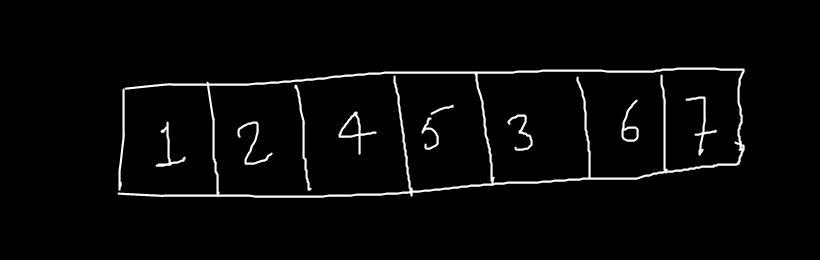
The answer for this Example is:

Initialize an Empty Arraylist as well as stack. and make a variable of TreeNode type current and assign the value of root into this variable for the traversing.

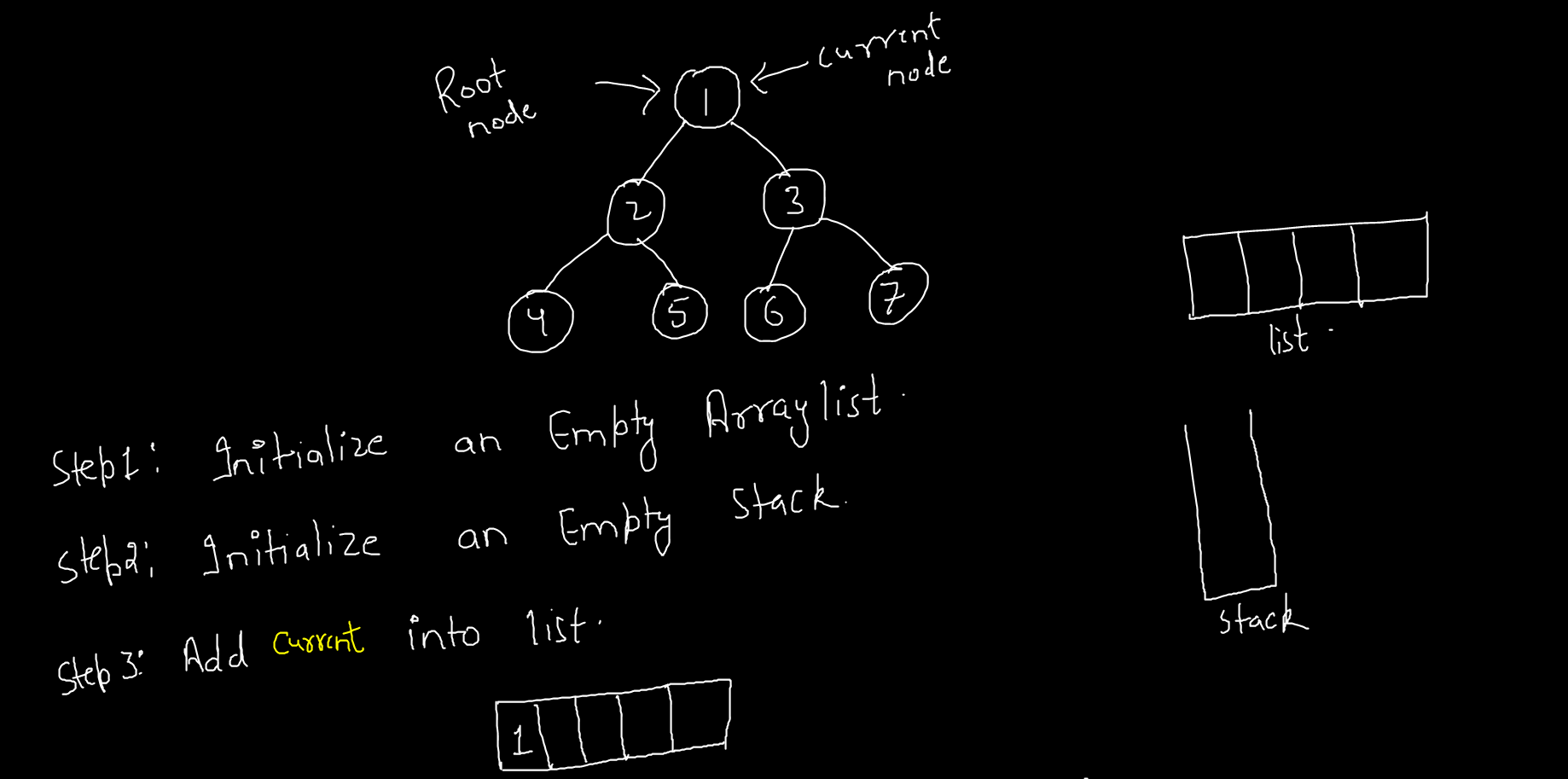
 List<Integer> result = new ArrayList<>();
 Stack<TreeNode> stack = new Stack<>();
 TreeNode current = root;
 if (root == null)
     return result;

Now, Traverse the whole tree using stack. and to traverse all node we are using loop and not recursion.

Check for the current node if the current node is not null than add the value of the current node in the list.

and this will be check for all nodes so it is inside the loop.

We will run the loops while the stack is not empty. if stack is empty than it means we have traverse all the node in the tree.

 while (!stack.isEmpty() || current != null) {
  if (current != null) {
      // Process the current node and add its value to the result
      result.add(current.val);
    }

Check the Right Child of the Current Node. if exists then push in the stack otherwise not.

We will check the right child for every node in the tree and push into the stack if exists.

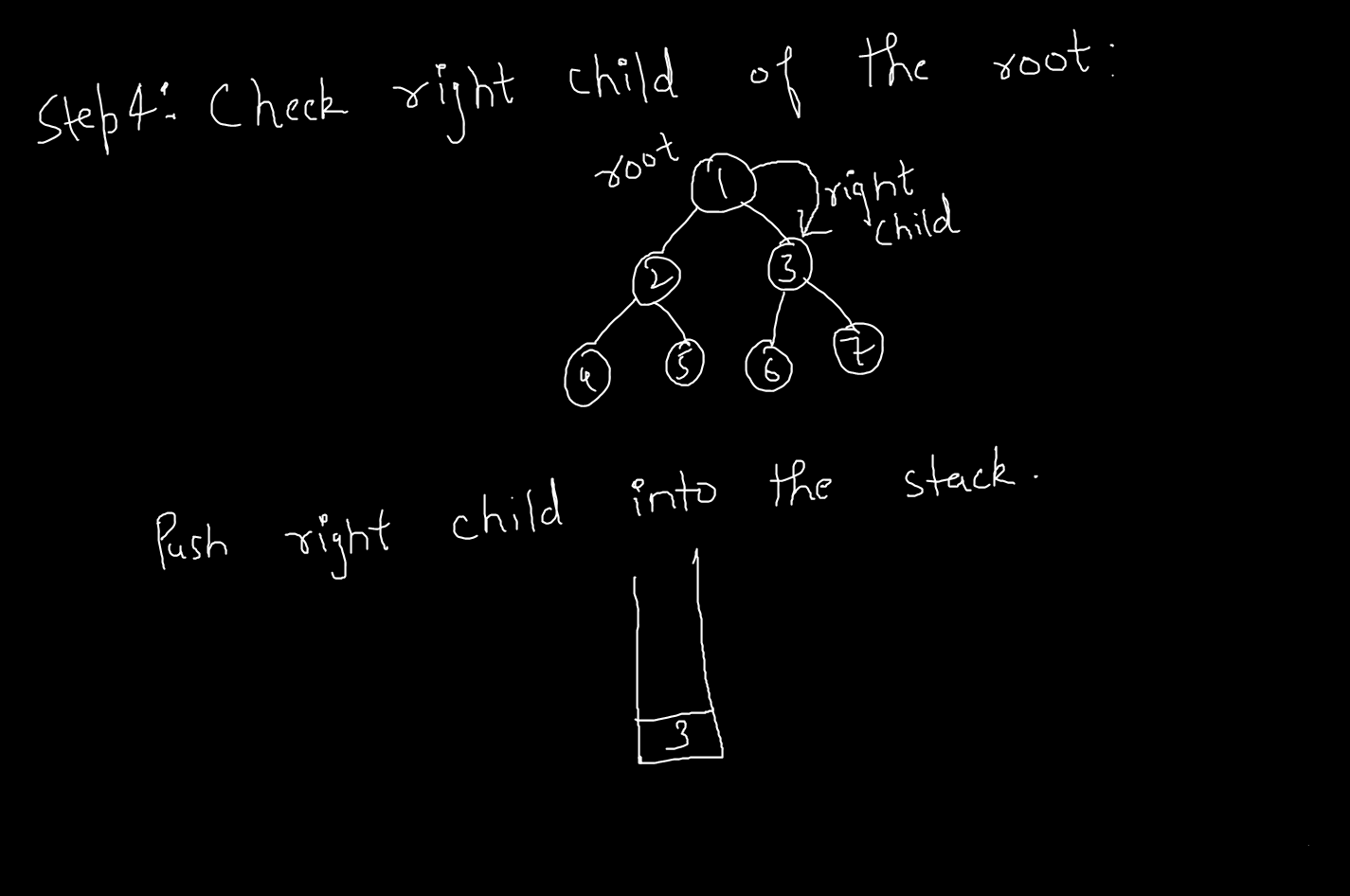
 if (current.right != null) {
     stack.push(current.right);
     }

Check For the left child of the current node if exists then move to that node by making the left node current as shown and code below.

We will check the left child of every node in the tree to make the next current node.

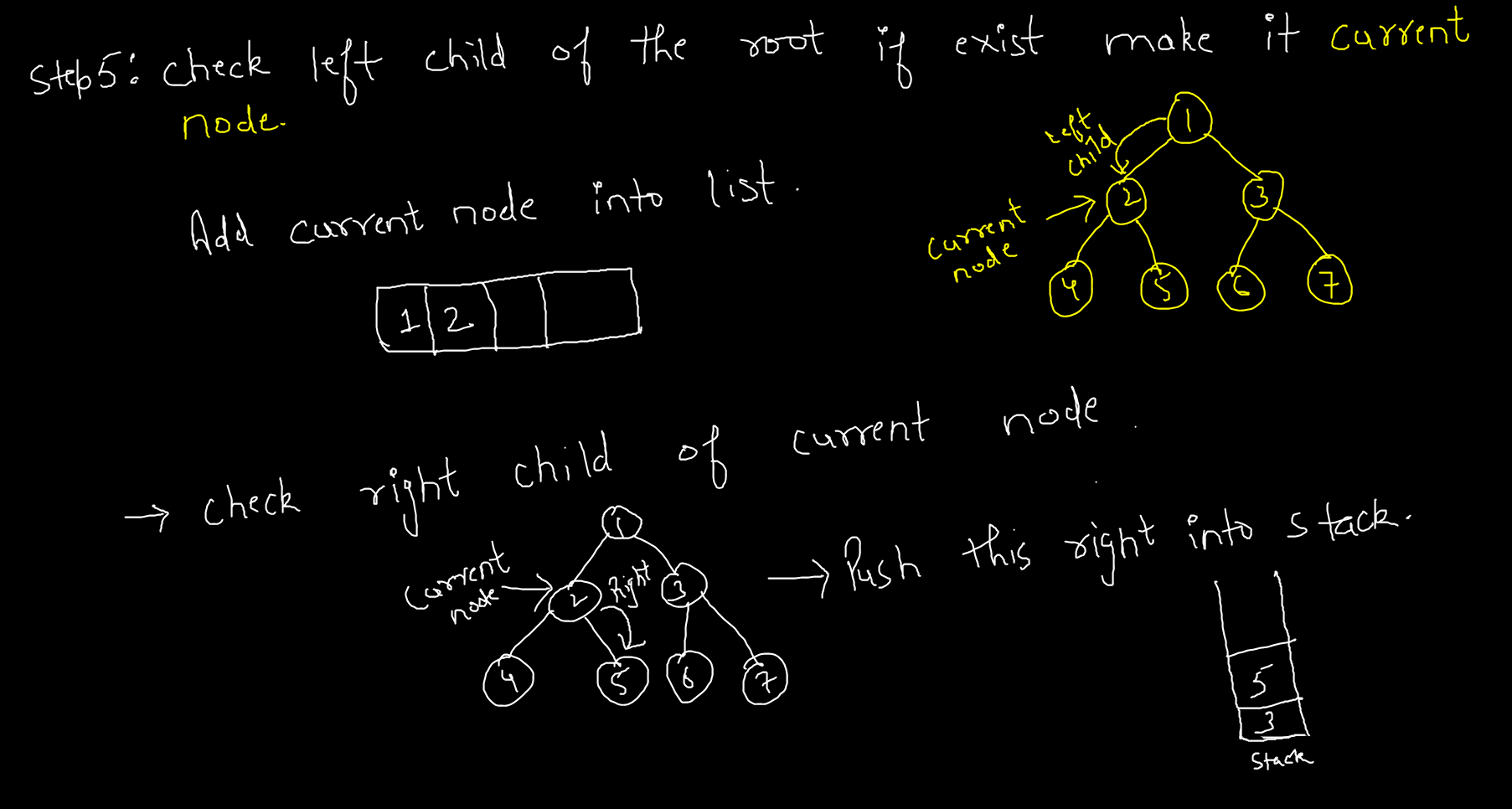
    // Move to the left child
    current = current.left;

Now if the current is not null then again its value add into the list.

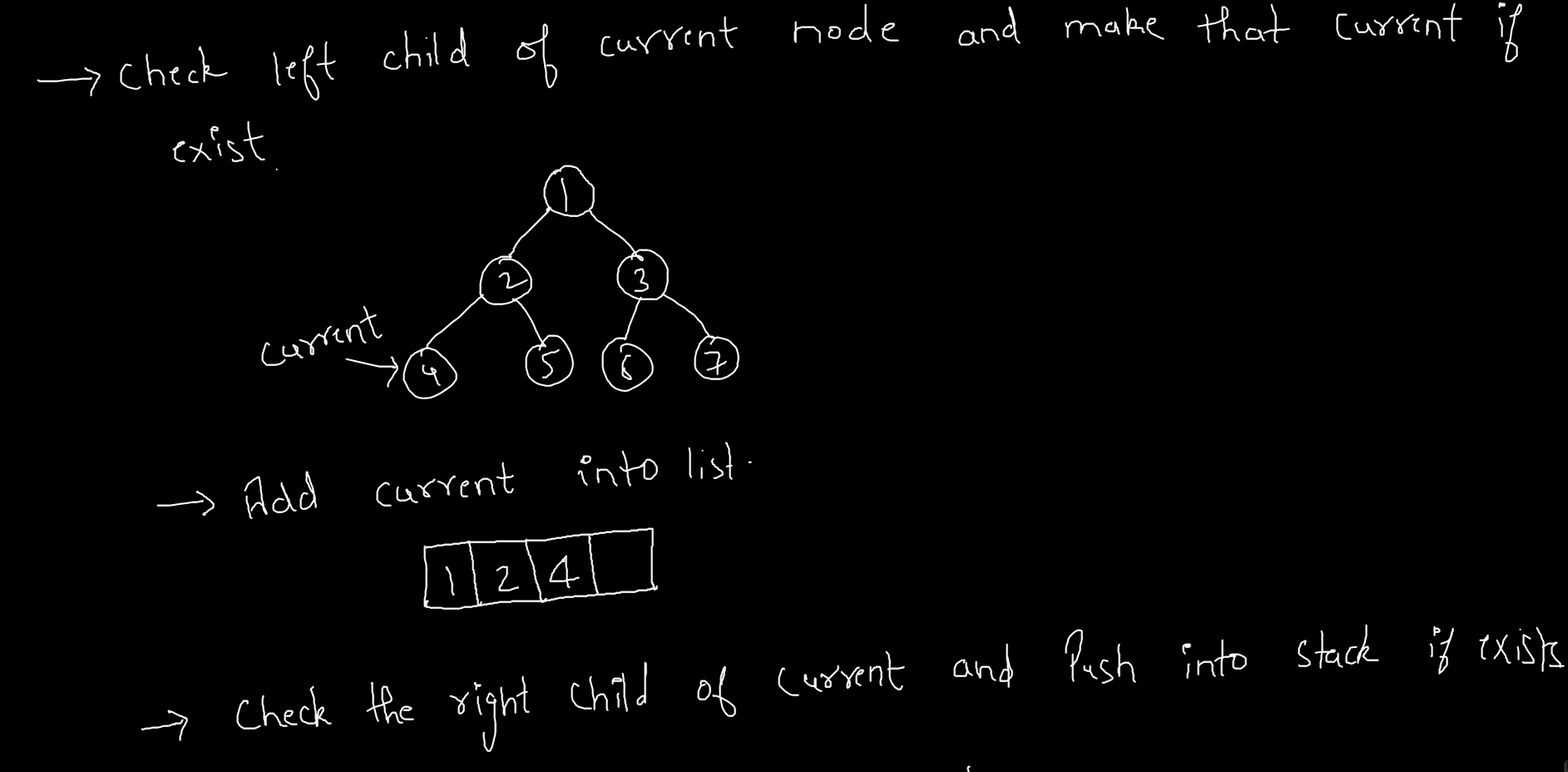
If the right and left both children are null then pop the element from the stack and make it current and then repeat the same, check the right of the node if exists then push into the stack and move to the left child by making the left child current node.

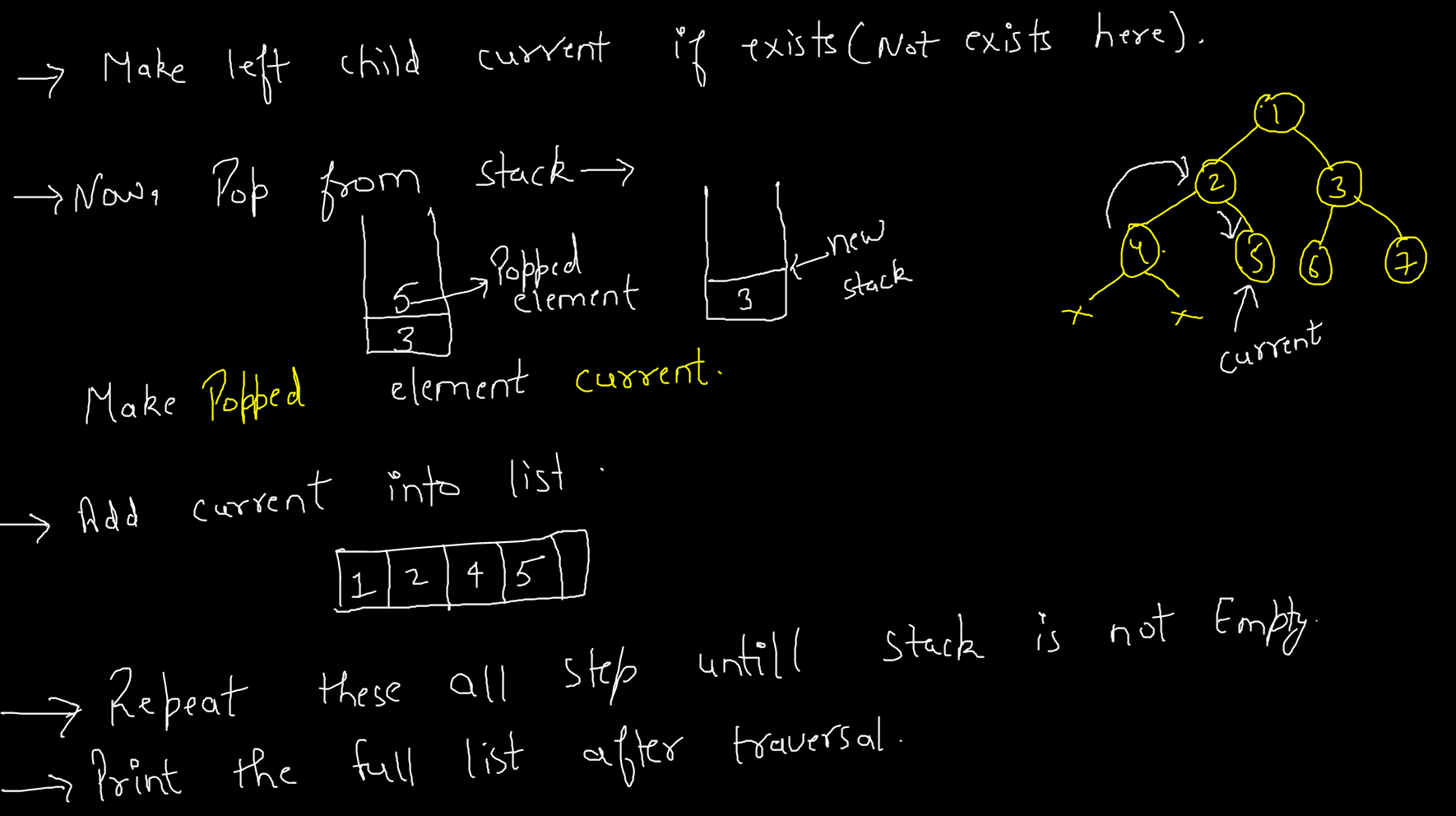
pop the top element from the stack and make it current as:

current = stack.pop();

After traversing the whole tree or after this loop finishing simply print the whole list to get the answer of traversal.

System.out.println("Preorder Traversal: " +  list);

Complete Code for Preorder Traversal Using Loops:

import java.util.*;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int x) {
        val = x;
    }
}

public class PreorderTraversal {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null)
            return result;

        Stack<TreeNode> stack = new Stack<>();
        TreeNode current = root;

        // Traverse the tree using a stack
        while (!stack.isEmpty() || current != null) {
            if (current != null) {
                // Process the current node and add its value to the result
                result.add(current.val);

                // Push the right child onto the stack first
                if (current.right != null) {
                    stack.push(current.right);
                }

                // Move to the left child
                current = current.left;
            } else {
                // If there's no left child, pop a node from the stack
                current = stack.pop();
            }
        }

        return result;
    }

    public static void main(String[] args) {
        // Example usage:
        // Create a binary tree
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.left.left = new TreeNode(4);
        root.left.right = new TreeNode(5);

        // Perform preorder traversal
        PreorderTraversal traversal = new PreorderTraversal();
        List<Integer> preorder = traversal.preorderTraversal(root);
        System.out.println("Preorder Traversal: " + preorder);
    }
}

Let's Run this code and Notice the Answer of this:

Preorder Traversal: [1, 2, 4, 5, 3, 6, 7]

Lets Discuss the Time  and Space Complexity of this Solution:

We have taken a stack in this solution of size n and an Arraylist also of size n so the total space required for this O(n);

In the Term of Time Complexity we have use only a loop to traverse all the nodes present in the tree so the total time taken by this is O(n);